Properties of Continuous Support Function Hahn Banach

For a mathematician, or more precisely for someone with a bit of training in functional analysis, support vector machines are probably the most relevant ML topic in their lives, given its dependence on various functional-analytic concepts like the separating hyperplane theorem, which is logically equivalent to the famous Hahn-Banach theorem.

Support vector machines (SVMs) are a method of classification in (usually) high-dimensional spaces that findseparating hyperplanes between groups of data. That is to say, if you have two groups of data in a high dimension $n$, we wish to find a hyperplane of dimension $(n-1)$ that serves as a "border" between the groups. Extensions of SVMs allow them to work with more than two classes, generate regression models (essentially, models of data relationships), and look for outliers to our data set. SVMs do this by relying on two main functional-analytic ideas:

• separating hyperplanes: a separating hyperplane is a hyperplane separating two groups as seen in this picture:

  

  
  The separating hyperplane theorem states that for two disjoint convex sets, we canalways find a hyperplane that separates them, with a certain well-defined gap if the convex sets are closed (not necessarily the case if they are both open, as the gap can be infinitesimally small – pretend the two sets above are open and "squeeze" them closer to the line to see how this can happen).
• kernel trick: thekernel trick in ML theory refers to a quick, efficient method of mapping your data into a higher dimensional space such that we can use the above theorem – more often than not, a Hilbert space where we can compute inner products (a measure of similarity) between vectors. More on this later; the main motivator for why we need these kernel tricks is that sometimes the dimensions of our original data are not high enough to properly distinguish between relevant clusters. However, one can always map into a higher dimensional space where the differences will show up, so that we may classify our data more accurately within this new space. (Consider that if there didnot exist a higher dimensional space – i.e. by extra added parameters/dimensions – where we could differentiate between two data points, then the points would effectively be the same anyway). As an illustration, consider the following image that I have blatantly ripped off from NYU's Langone Medical Center website, where they consider an SVM approach to classifying epidemiological groups in cancer research:

  

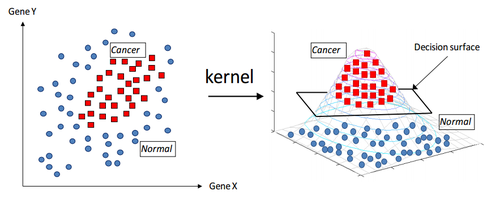
First, some preliminary comments: the motivation for SVMs and classification in general is the same that we had with clustering, but it should be mentioned that SVMs are asupervised learning technique as opposed to clustering (by, say, $k$-means, amongst other algorithms), which isunsupervised. The terms mean pretty much exactly what one would expect them to mean: supervised algorithms are those that have "correct answers" labelled in the data during a training stage, and the algorithm can be trained to derive correct or approximately-correct inferences in future data. Unsupervised algorithms are those where there is no implicit "answer" in the data. Supervised learning means your algorithm is essentially learning by example, having had some training; unsupervised learning means it is looking for meaningful patterns in raw, unlabelled data. Of course, there are degrees of training involved, and one could subdivide supervised learning into subfields depending on how much assistance the learning algorithms have.

Anyway, let's set the context for the general problem that SVMs are supposed to tackle. We of course have a large number of data points where each data point is an $n$-dimensional vector (for some $n$ depending on the number offeatures orattributes your data possess); let's assume you can "see" two distinct groups of data here that are clustered around two somewhat different general spatial areas, and further that these two groups are labelled in the training data (so that you can compute which group each test datum belongs to). At this point, we have to ask some questions about the nature of these groups of data points.

• From the separating hyperplane theorem, we know that if we take theconvex hull of each of these groups and theydo not intersect, there must exist a hyperplane separating them, and indeed a hyperplane that is of equal distance between the two groups (so that the plane is right in the "middle" of them). Of course, the theorem is purely existential – after all, it relies on a weak form of the axiom of choice for a proof. How do we find this plane? Consider the scenario where the convex hulls of the two groups of data do not intersect each other. Then it turns out that we can convert the problem into one of optimization, since we wish to find a linear function $w \cdot x + b$ defining a plane that maximizes the average distance from the plane to each data point. I won't get into the details since it is a bit lengthy to type up, but this is derived in Andrew Ng's notes, and is done in practice by things like the SMO algorithm, which also works for soft margins (see next bulletpoint).
• If the convex hulls have a non-empty intersection, but the intersection is rather small, not all hope is lost – essentially, we can still find a separating plane, but class/group predictions wouldn't be very accurate for data points falling close to the plane. We can hence use a "soft" approach by modifying the above technique with an extra parameter. This is called thesoft marginmethod and introduces the extra parameter(s), which you can consider to be a measure of miscalculation, into the optimization problem. We then want to optimize while minimizing miscalculation. For more information, see the link.
• The last scenario is the one that necessitates using akernel trick: if the two groups of data cannot be appropriately separated by a hyperplane, say, if the data is best separated by some sort of curve or manifold, then we will map all our data into a Hilbert space with dimension high enough to allow for a linear function (i.e. a plane) to act as the separating function. Recall from linear algebra that a matrix can serve as an inner product if and only if it is positive definite; likewise, if we're going to use our kernel function to act as a way of "transporting" dot products in a low dimensional space to dot products in a high dimensional space, we're going to want a positive definite kernel. (See the example below for further details.)

Here's a worked example of a toy(-ish) model in which we want to use the kernel trick. Say you have pairs $(x_i,y_i)$ where the $x_i \in X$ are your data points, and the $y_i \in \{-1,+1\}$ – theresponses – tell you whether a data point is in the first group (negative) or the second group (positive). These are your supervised training examples. In general, to have our machine actually "learn", we want to be able to throw our program a new point $x$ and have it guess $y$, i.e. whether it is in the first or second group. We hence want to put a measure of "similarity" on the data space $X$; the most obvious similarity measure that springs to mind is the inner product, i.e. the dot product, since it satisfies a decently intuitive notion of similarity (symmetric, positive definite, etc.). But if we have the nonlinearity issues that we described and the points are all in a jumble, everything seems to be similar to everything else; is there a different inner product we can use where differences will be more apparent? Maybe there is a function $F: X \to H$ (for $H$ a Hilbert space, i.e. a vector space with an inner product on it), such that $F$ (called thefeature map) takes the data to a higher (possibly infinite!) dimensional context (called thefeature space), so that $\langle F(x'), F(x'') \rangle$ is an inner product thatdoes distinguish our data points. Now since this is an inner product, we also have a corresponding positive-definite kernel function $K$ such that

$$K(x',x'') = \langle F(x'),F(x'') \rangle$$.

In practice, there is a collection of commonly used kernel functions that we attempt to use; popular ones include the radial and polynomial kernels.

Now let's assume that this feature space is "nice enough" to let us distinguish our points. What should we do now? Well, we have our new data point $x$ and we want to find a nice way of predicting $y \in \{-1,+1\}$. Assume for now that the groups are "centered" at the origin of the feature in some suitable way; it then makes sense to set

$$y = sign(\frac{1}{n}\sum_{i: y_i = +1}K(x,x_i) - \frac{1}{n}\sum_{i: y_i = -1}K(x,x_i))$$,

i.e. the sign of the difference between "the average similarity of $x$ to the positive group" and "the average similarity of $x$ to the negative group" – so that the sign of this difference is positive if $x$ is closer to the positive group, and negative if it is closer to the negative group. When the two groups are translated away from the origin, we will have an additive term inside the argument of the sign function; the additive term is given by a suitable averaging of the elements in the two groups.

Going back to the assumption that our feature space is nice enough to distinguish our previously indistinguishable groups of data, we will now remark that in general, there is no overall method to find such a space, since the requirements differ depending on context. However, the point is that the kernel iseasy to compute, and the feature map may behard to compute; so we can try a whole bunch of different kernels until one of them does linearly separate the data. Of course, choosing something too large or overshooting is possible too.

I'll stop the discussion here as I think this gives enough of a cursory introduction to the purpose and implementation of SVMs. Further details and applications may be touched upon in future posts. To summarize, sometimes we have a desire to separate groups of data in a high dimensional space; support vector machines are algorithms/programs/techniques which do just that, by finding a hyperplane of interest that acts as a "boundary" (with nice linear (and hence, computable) properties, since they are, after all, just planes in euclidean space) between the two groups. The fact that we can actually construct these planes is implied by the separating hyperplane theorem, and our ability to choose a high enough dimension for the space in which we embed the data vectors comes from our ability to perform a kernel trick. Finding a constructive way of obtaining this hyperplane of interest (once we've chosen a relevant space for the data) is done by reducing it to an optimization problem, which may be solved by the iterative SMO algorithm.

There is one last thing that I wanted to mention, and I didn't have a good idea of where to place it. As an example of a rather interesting data classification problem using high-dimensional feature spaces that I had seen during a guest lecture in a colloquium, I would like to mention the inspiring and interesting work of William Sethares, who has some relevant papers to this topic listed at his DBLP entry. Of special relevance is The Topology of Musical Data (Budney, Sethares), in which musical pieces are embedded into a high dimensional metric space with a non-euclidean metric. For example, some "coordinates" in this space may represent adjacent musical notes, or numerical data in the associated MIDI file of the piece. They then find ways of finding topological structures in this space that are associated with music-theoretic structures – for example, the circle of fifths diagram that represents the relationships between key signatures of the notes of the chromatic scale are manifested in the data as a torus. Very interesting stuff, indeed, though I can't claim to be an expert.

The next post will be on the application of variational methods towards approximations of probability distributions and inspirations from statistical physics. Cheers!

shieldsyoursider.blogspot.com

Source: https://metalanguages.tumblr.com/post/76432313115/machine-learning-iii-support-vector-machines-and

Share this post